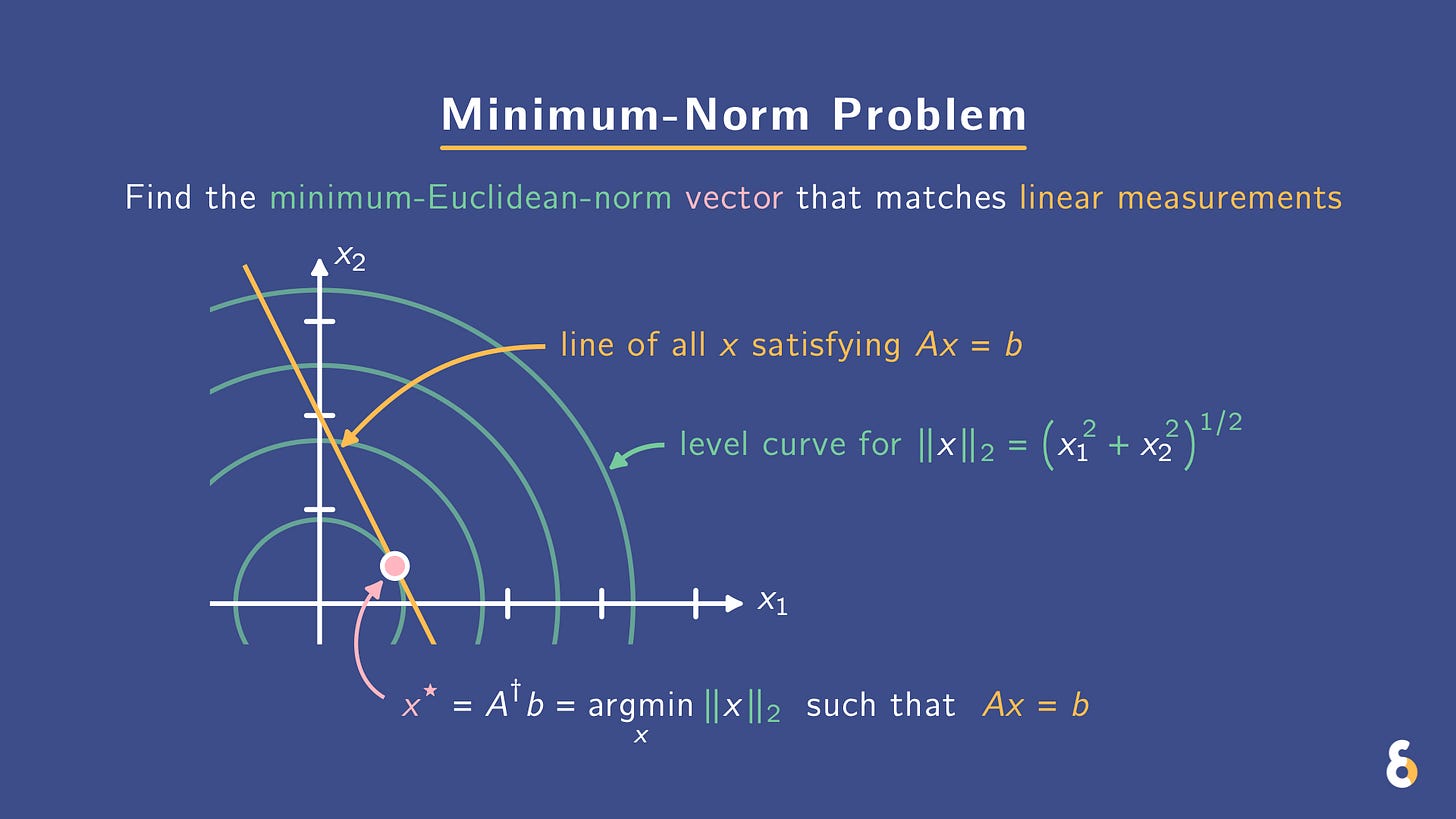
While ℓ₁ seeks corners, ℓ₂ seeks calm. Exact constraints, minimal energy. Get it via the pseudoinverse.
The problem
min ‖x‖₂ with Ax=b
of finding the minimum-norm solution picks, among all exact fits, the shortest / lowest-energy vector. Where ℓ₁ (basis pursuit) prefers sparse vectors, ℓ₂ prefers low-energy vectors as the tie-breaker when many solutions exist.
If Ax=b is consistent, the unique minimum-norm solution is x = A†b where A† is the Moore-Penrose pseudoinverse. How can you compute this? Take the singular value decomposition A = UΣV^⊤, invert only the nonzero singular values, and swap U and V to get A† = VΣ† U^⊤. In the common full-row-rank case (more columns than rows), this reduces to
A† = A^⊤ (AA^⊤)^(-1).
The pseudoinverse projects the vector 0 onto the affine set {x : Ax = b}. By definition of a projection, the point you land on is the closest (minimum-norm) solution.
📝 Brief derivation
L(x,𝜆) = 0.5 ∥x∥^2 + 𝜆 * (Ax-b) ⇒ x = A^⊤ 𝜆.
Plug in b = Ax = A(A^⊤ 𝜆) to get x = A^⊤(AA^⊤)^(-1) b.
⚠️ What to Avoid
If constraints are noisy or inconsistent, switch to least squares or add regularization (e.g. Tikhonov, ridge).
⸻
📚 Further Reading