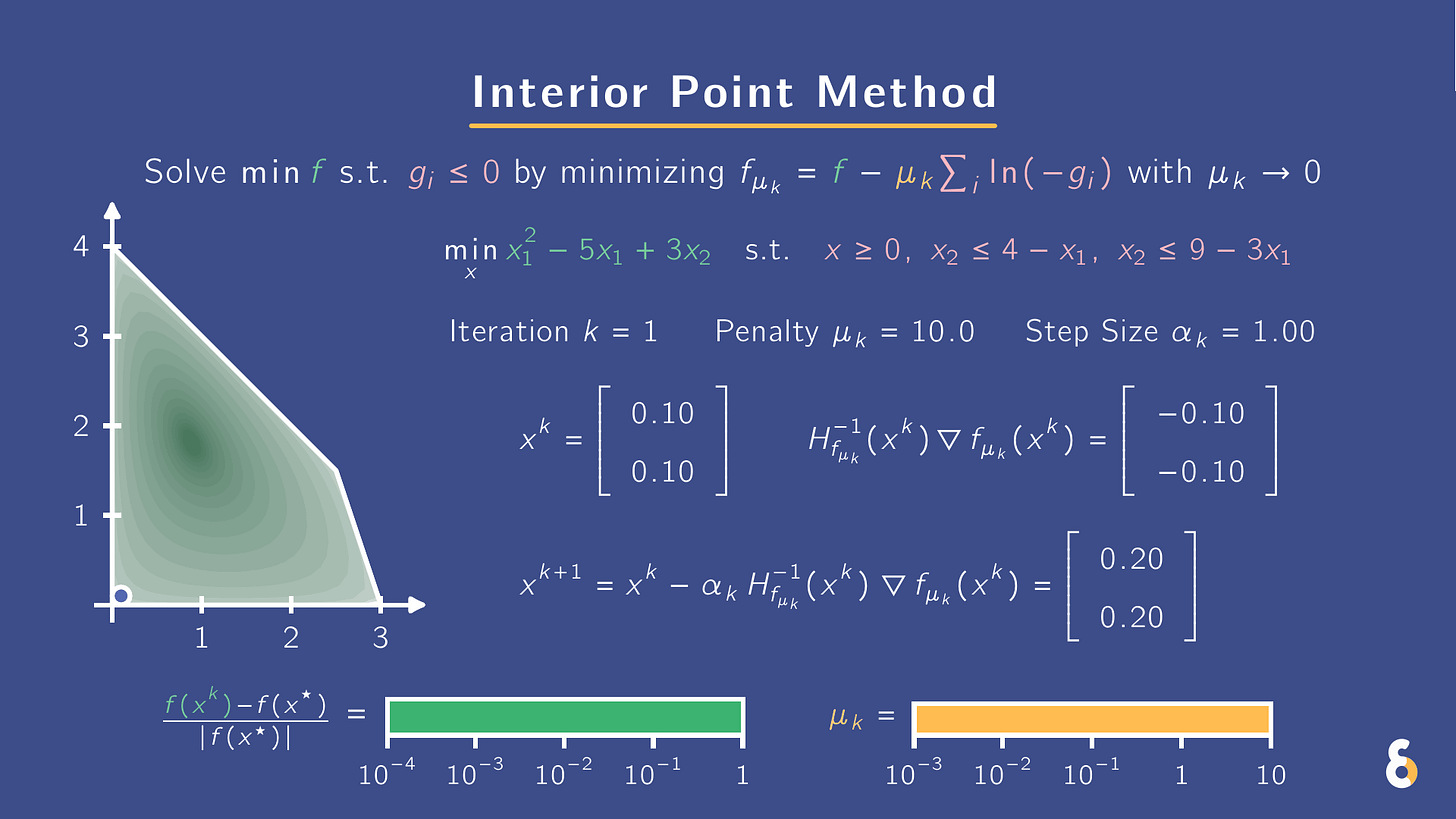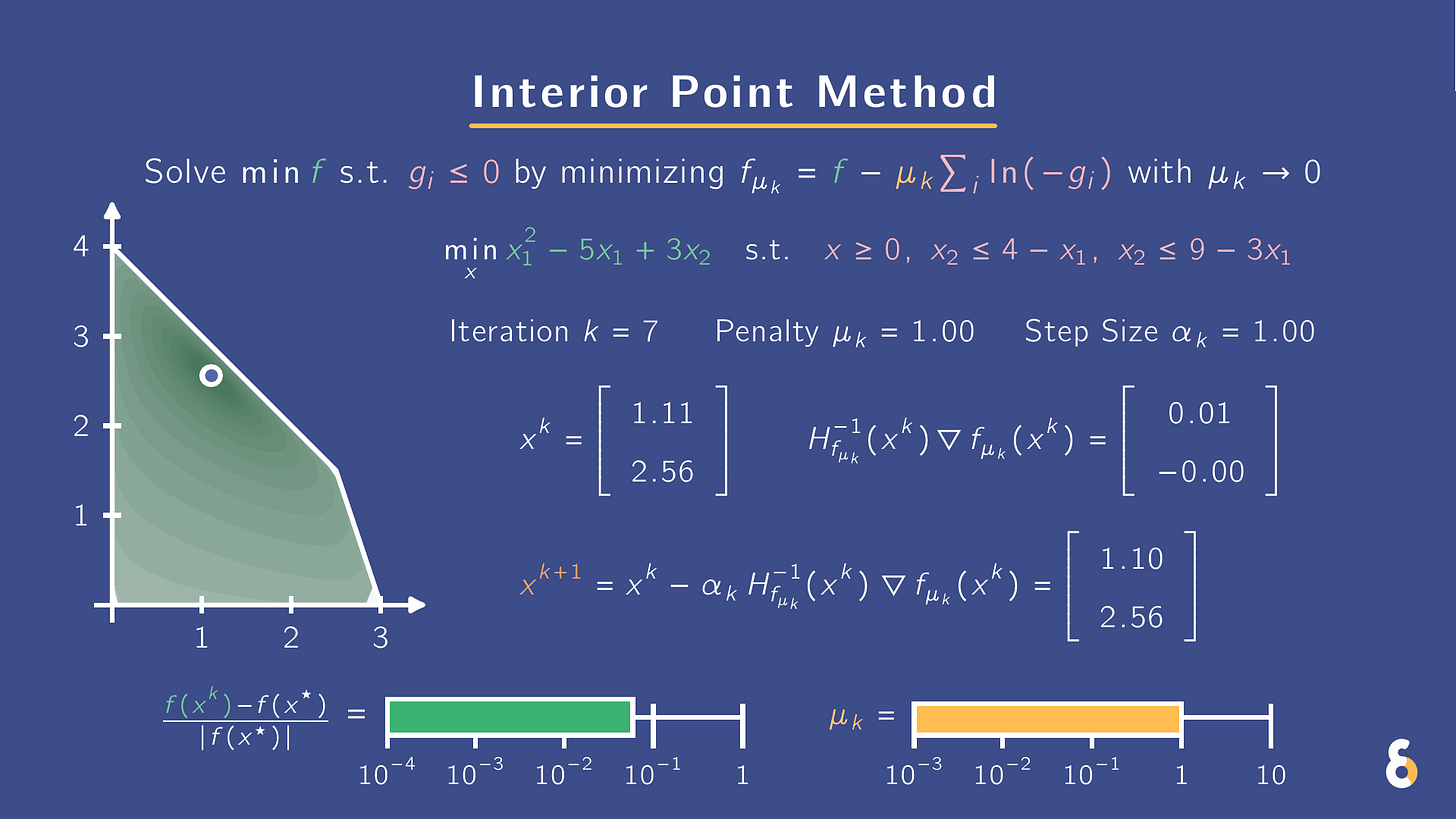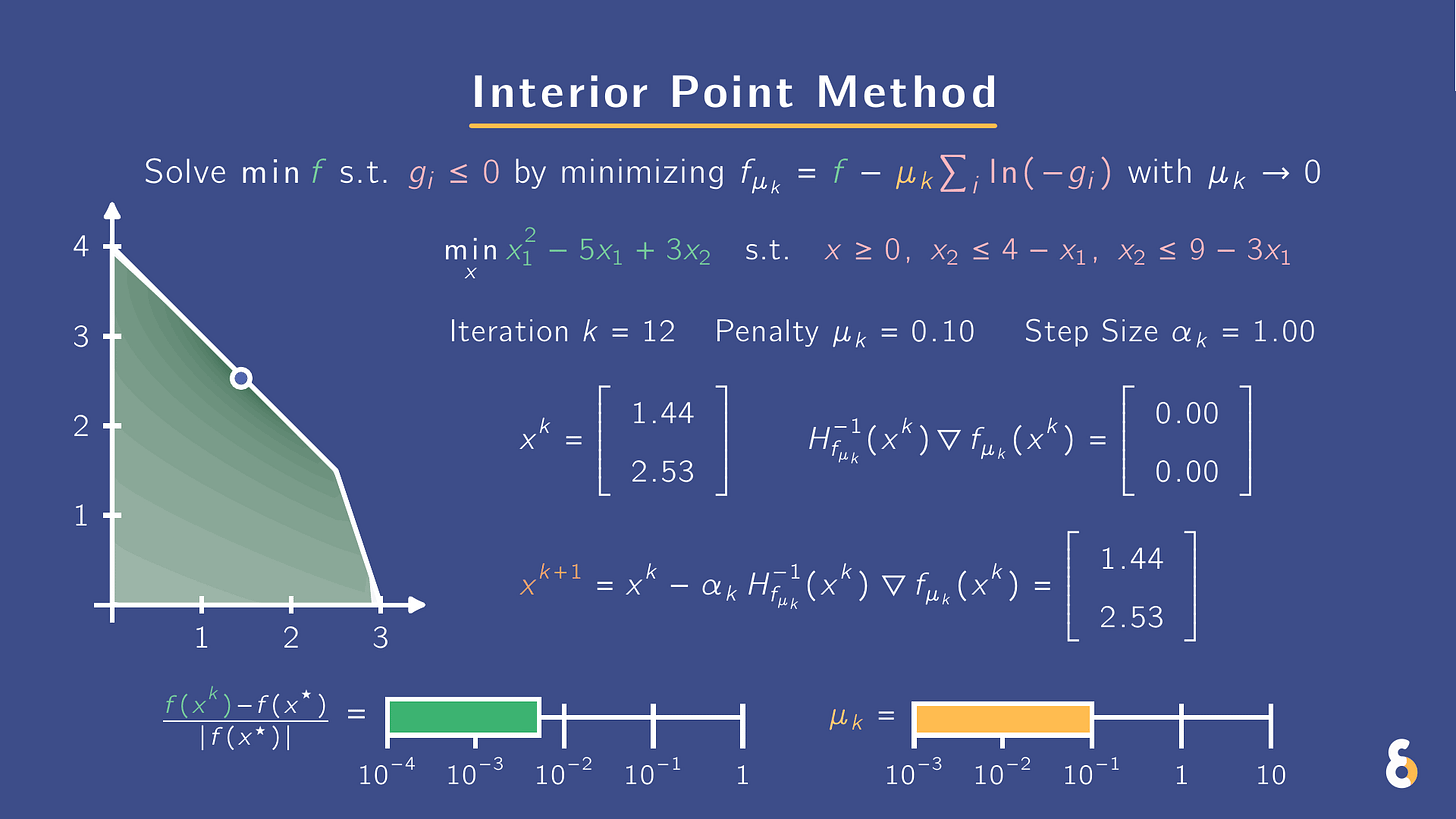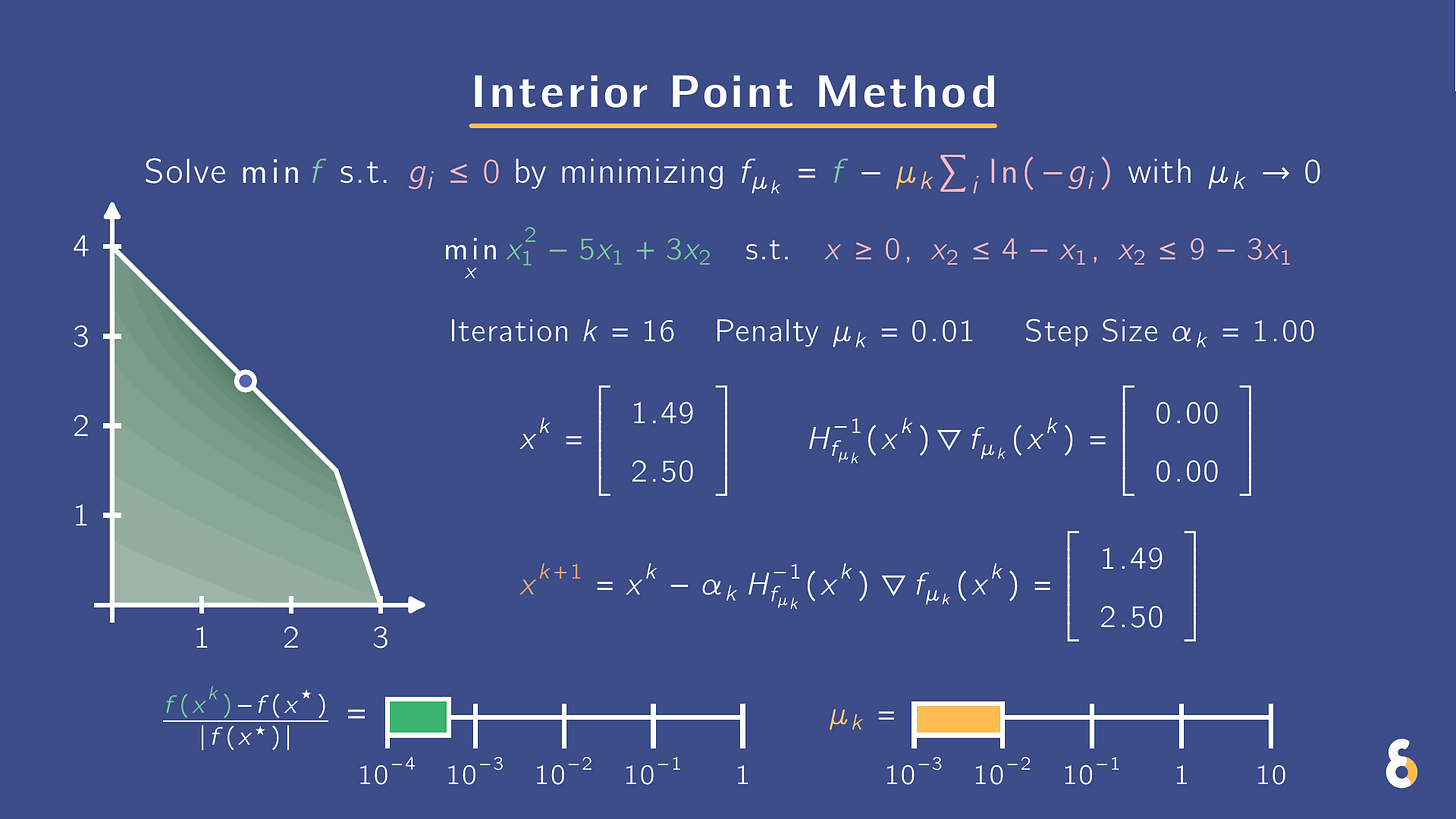
Newton struggling with constraints? Use IPMs. They turn gᵢ(x) ≤ 0 into smooth penalties. Same solution, friendlier landscape.
In the .gif above, I minimize f(x) under gᵢ(x) ≤ 0 via an interior point method (IPM). Namely, I add a barrier term to the objective f(x) and minimize the sum
f(x) − μ Σᵢ log(−gᵢ(x)),
with μ > 0 shrinking over time. Log barriers blow up to ∞ at constraint boundaries, making iterates avoid gᵢ(x) = 0 and stay in the interior of the feasible set {x : gᵢ(x) ≤ 0 for all i}. The path of minimizers as μ shrinks (i.e. central path) slides toward the solution of the original problem.
This barrier form makes the landscape smooth and friendly to Newton steps, even with many constraints. In the .gif, a modified Newton method is used where the step size is reduced until the candidate update is feasible. Green shading shows the landscape for the sum of the objective and barrier terms.
Where have you seen interior point methods applied?
⸻
p.s. Credit is due to Yaoguo Li for suggesting an interior point post and to Tom Yeh for inspiring writing out individual steps in the algorithm. I recommend reading Tom’s Substack: AI by Hand