The fastest path isn’t a straight line. In 1696, Johann Bernoulli posed a riddle. Newton solved it overnight.
The challenge was simple to state:
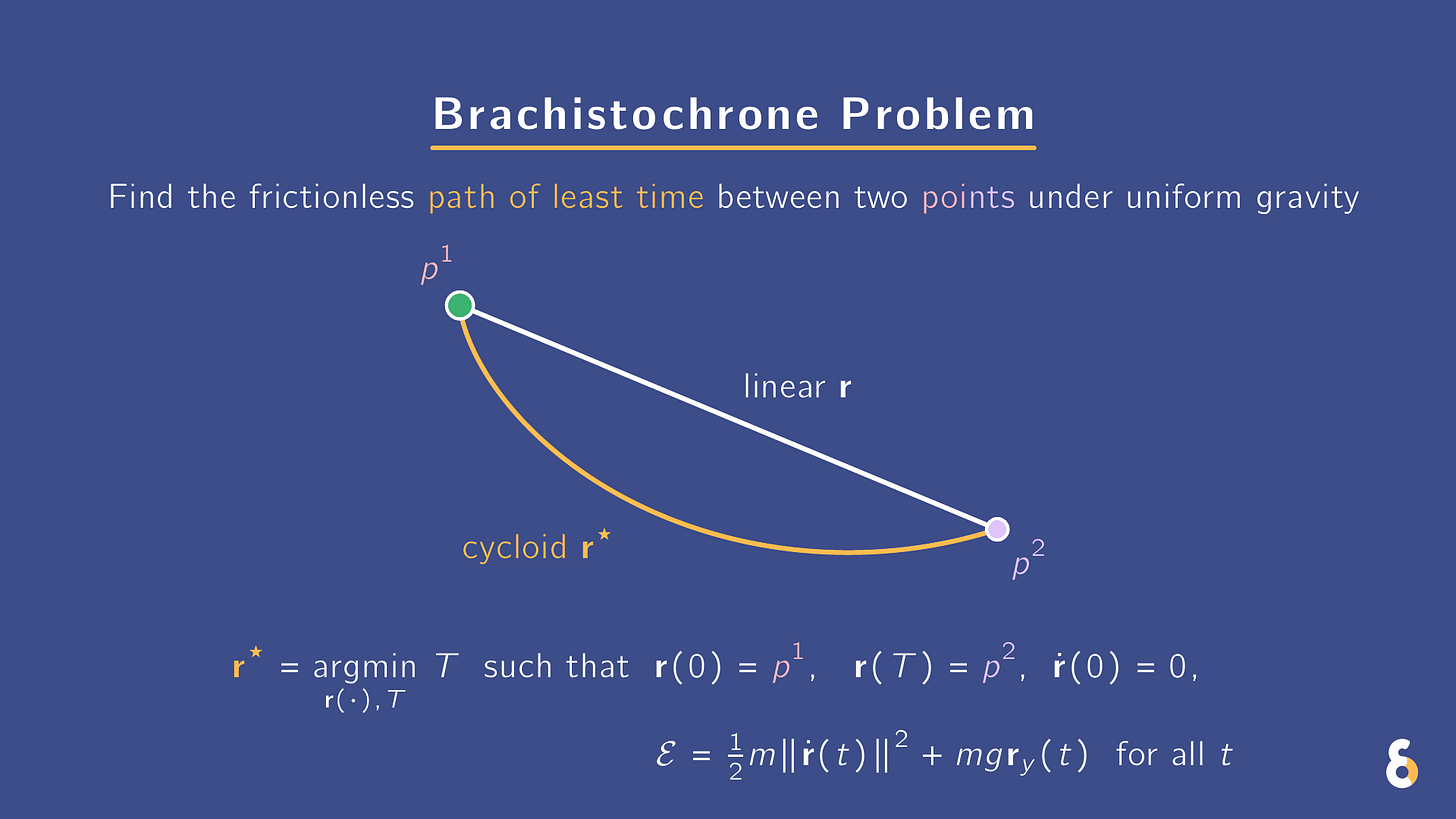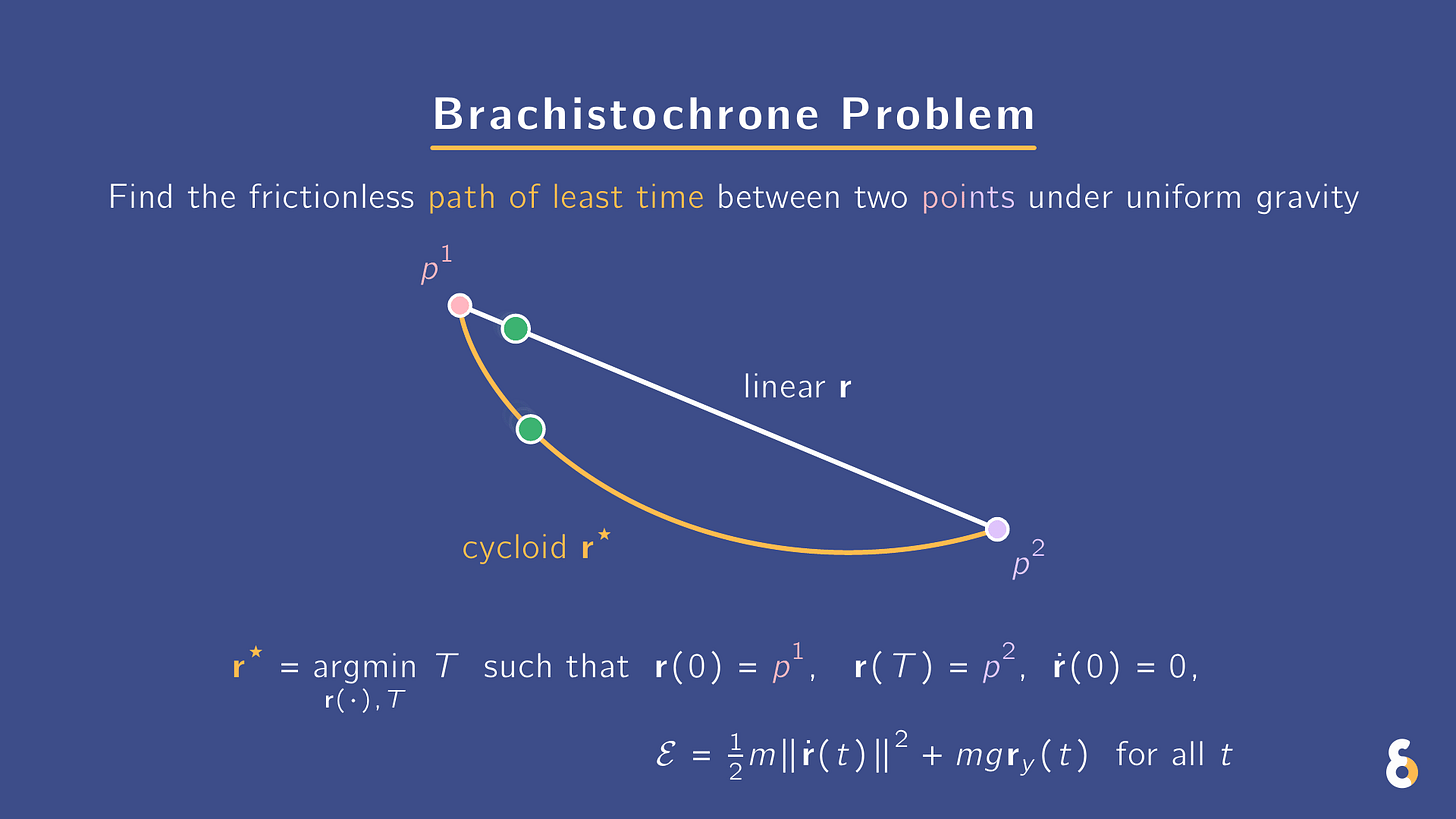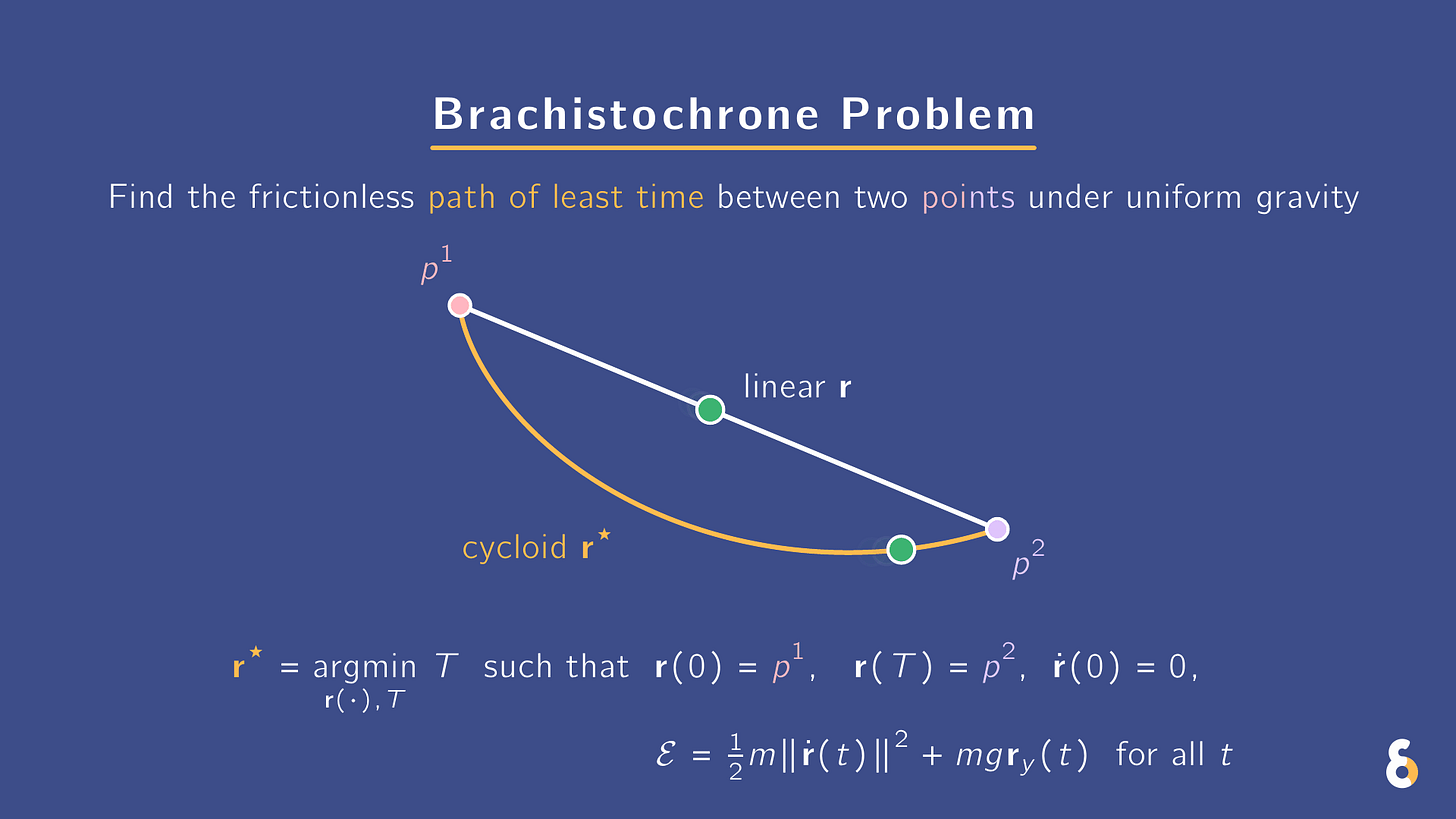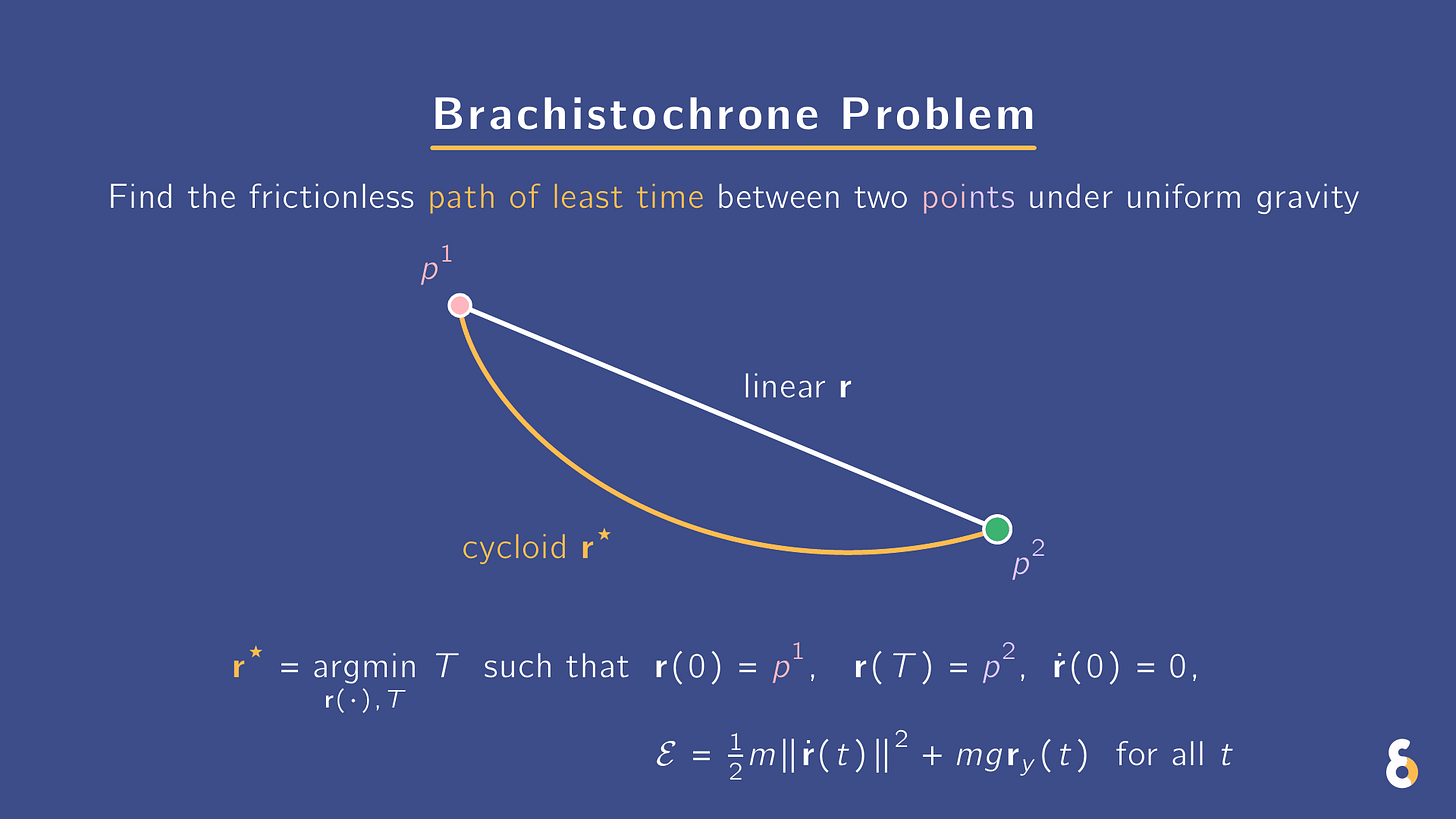
Between two points at different heights, what curve gets a bead down fastest under gravity?
This is the brachistochrone problem, aimed at finding the “shortest-time curve”. Newton, given this at the end of a workday, reportedly solved it by morning.
The surprising answer:
not a straight line,
not a circle,
but a cycloid,
the curve traced by a rolling wheel.
Why does this matter for optimization? Because the decision variable isn’t a number or a vector. It’s an entire function y(x). We’re minimizing an integral functional (the total travel time) over an infinite-dimensional space of curves.
This challenge helped birth* the calculus of variations, a precursor to modern optimal control and PDE-constrained optimization. It’s a vivid reminder that optimization can shape not just numbers but entire paths, shapes, and systems.
*Newton's minimal resistance problem from a decade earlier is the first known problem to be stated and solved using the calculus of variations.
p.s. Upon seeing Newton's anonymous solution, Bernoulli is said to have known it was Newton as he "recognizes a lion from his claw mark."