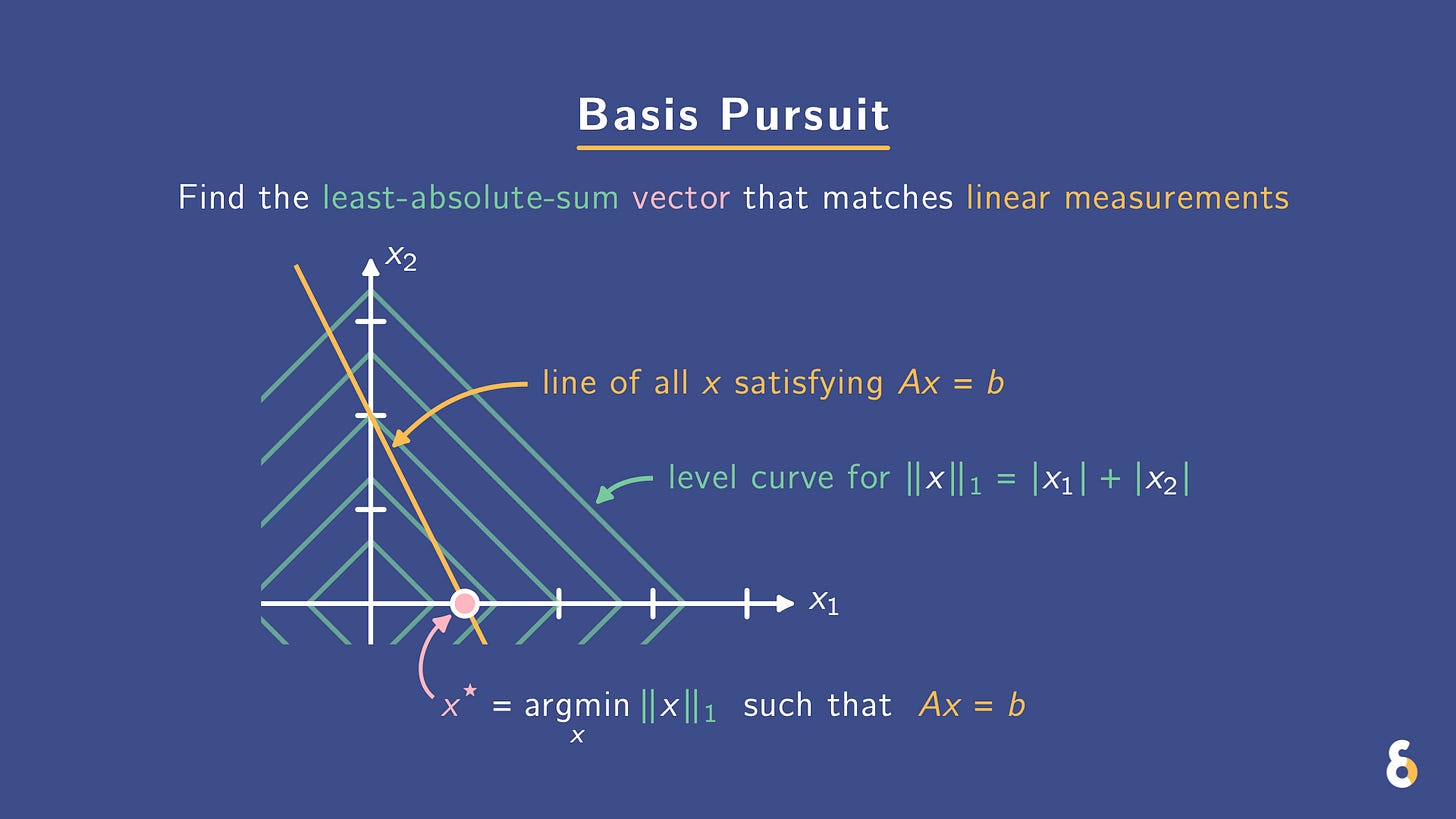
Corners beat circles. The L₁ diamond selects low absolute-sum (often sparse) solutions.
Equality constraints can leave many exact-fit solutions. L₁ is the principled tie-breaker: pick the vector with the least absolute sum. Geometry: the L₁ ball is a diamond; its corners align with the axes, so intersecting with Ax = b tends to land on a corner, driving many entries to zero. In contrast, L₂ balls are circles.
Formally, the basis pursuit problem is
minimize ∥x∥₁ subject to Ax = b.
This reveals structure from few measurements and, under standard compressed sensing conditions, matches the truly sparse solution. With noise, relax the fit (basis pursuit denoise) or add a penalty (LASSO).
Applications:
🔹 MRI with exact data consistency (noiseless k-space)
🔹 Seismic interpolation (equality on observed samples)
🔹 Sparse spike recovery from exact Fourier samples
🔹 Noiseless sparse coding in overcomplete dictionaries